Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
Tags
- plan
- Developer
- Mac
- php
- 개발
- 프로그래밍 언어론
- windows
- CodeIgniter
- Java
- 개인서버
- 정보처리기능사
- React
- study
- WPF
- 외부접속
- 방화벽
- bootcamp
- 개발공부
- 홈서버
- 매크로
- 220821
- CSS
- cording
- 프로그래밍언어론
- knockon
- 자격증
- 오답풀이
- git
- html
- C
Archives
- Today
- Total
bunta의 보조기억장치
[1주차 TIL] KnockOn Bootcamp 트리 본문
반응형
💡 트리(Tree)란?
트리(Tree)란 자료구조 중 한 종류로, 하나의 노드를 루트 노드(Root Node)를 시작으로 자식 노드(Child Node)들이 연결되어 나무처럼 가지를 뻗어 나가는 계층적 구조이다.
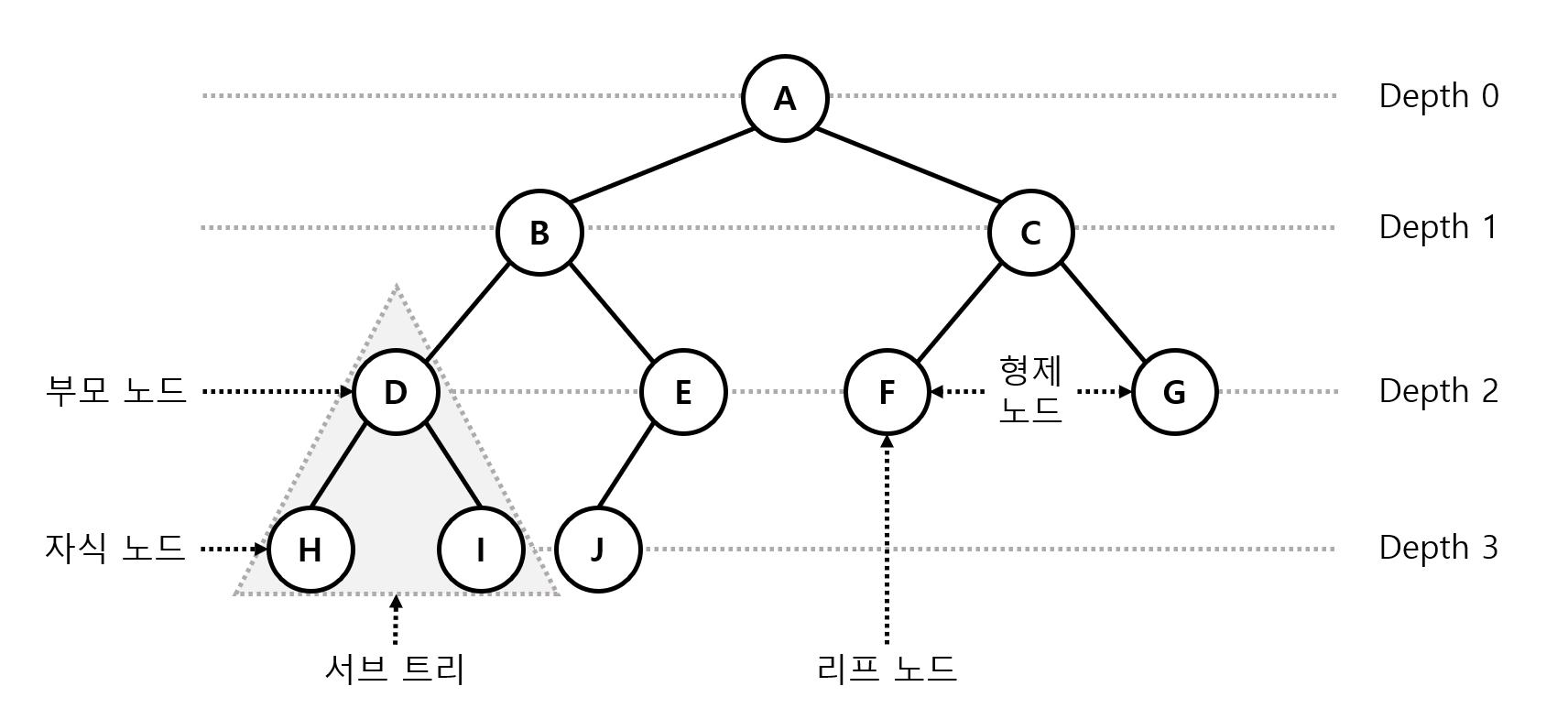
트리의 기본 개념
- 루트(Root) : 트리의 가장 위에 있는 시작 노드
- 노드(Node) : 트리의 각 요소(데이터를 담고 있음)
- 간선(Edge) : 노드와 노드를 연결하는 선
- 부모(Parent) 노드 : 다른 노드를 가리키는 노드
- 자식(Child) 노드 : 부모 노드에 의해 연결된 하위 노드
- 형제(Sibling) 노드 : 같은 부모 노드를 가진 노드들
- 리프(Leaf) 노드 : 자식 노드가 없는 노드(끝 노드)
- 서브트리(Subtree) : 하나의 노드와 그 하위 노드들로 이루어진 트리
- 깊이(Depth) : 루트 노드에서 특정 노드까지의 거리(간선의 개수)
*루트 노드의 깊이는 0 - 트리 높이(Height) : 루트 노드에서 가장 깊은 리프 노드까지의 거리(=최대 깊이)
- 노드 높이(Height) : 해당 노드에서 가장 깊은 자식 노드까지의 거리
- 트리 차수(Degree) : 트리 내 모든 노드 중에서 가장 큰 차수 값
- 노드 차수(Degree) : 해당 노드가 가지고 있는 자식 노드의 수
트리의 특징
- 하나의 루트 노드에서 시작해 계층적으로 분기
- 노드 간에는 정확히 하나의 경로만 존재
- 비선형 구조 (1:N, N:N 가능)
🔎 이진 트리와 완전 이진 트리
이진 트리
모든 노드가 최대 두 개의 자식 노드를 가지고 있는 트리를 얘기한다.

완전 이진 트리
이진 트리와 마찬가지로 모든 노드가 최대 두 개의 자식 노드를 가지고 있으며, 마지막 레벨(최하단)을 제외한 모든 노드는 완전히 채워져 있어야 한다.
마지막 레벨의 노드들은 반드시 왼쪽부터 채워져 있어야 한다.

이진 탐색 트리
이진트리와 마찬가지로 모든 노드가 최대 두 개의 자식 노드를 가지고 있으며, 부모 노드의 왼쪽에는 부모 노드보다 작은 값의 자식 노드들이, 오른쪽에는 부모 노드보다 큰 값의 자식 노드들이 존재해야 한다.
또한 중복된 값을 허용하지 않는다.

✅ 이진 탐색 트리의 장점
- 탐색, 삽입, 삭제 속도가 빠름
(단, 트리가 균형 잡혀있는 경우) - 중위 순회를 하면 정렬된 결과를 얻을 수 있음
❌ 이진 탐색 트리의 단점
- 트리가 한쪽으로 치우친 경우 성능이 떨어짐
🔎 이진 트리 순회 방법
전위 순회(Pre-order)
[루트→왼쪽 →오른쪽] 순으로 노드를 방문
중위 순회(In-order)
왼쪽 → 루트→ 오른쪽 순으로 노드를 방문
후위 순회(Post-order)
왼쪽 → 오른쪽 → 루트 순으로 노드를 방문

🎯 트리 구현해보기
#include <stdio.h>
#include <stdlib.h>
// 트리 노드 구조체 정의
typedef struct TreeNode {
int data;
struct TreeNode* left;
struct TreeNode* right;
} TreeNode;
// 새 노드 생성 함수
TreeNode* createNode(int data)
{
TreeNode* newNode = (TreeNode*) malloc(sizeof(TreeNode));
if(newNode == NULL)
{
printf("mallocfailed\n");
return NULL;
}
newNode->data = data;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
// 트리에 노드 삽입(이진 탐색 트리 형태)
TreeNode* insert(TreeNode* root, int data)
{
if(root == NULL)
{
return createNode(data);
}
if(data < root->data)
{
root->left = insert(root->left, data);
}
else
{
root->right = insert(root->right, data);
}
return root;
}
// 중위 순회(In-order)
void inorder(TreeNode* root)
{
if(root != NULL)
{
inorder(root->left);
printf("%d ", root->data);
inorder(root->right);
}
}
// 전위 순회(Pre-order)
void preorder(TreeNode* root)
{
if(root != NULL)
{
printf("%d ", root->data);
preorder(root->left);
preorder(root->right);
}
}
// 후위 순회(Post-order)
void postorder(TreeNode* root)
{
if(root != NULL)
{
postorder(root->left);
postorder(root->right);
printf("%d ", root->data);
}
}
// 트리 메모리 해제
void freeTree(TreeNode* root)
{
if(root != NULL)
{
freeTree(root->left);
freeTree(root->right);
free(root);
}
}
int main()
{
TreeNode* root = NULL;
// 트리 구성
root = insert(root, 50);
insert(root, 30);
insert(root, 70);
insert(root, 20);
insert(root, 40);
insert(root, 60);
insert(root, 80);
printf("In-order: ");
inorder(root);
printf("\n");
printf("Pre-order: ");
preorder(root);
printf("\n");
printf("Post-order: ");
postorder(root);
printf("\n");
freeTree(root);
return 0;
}반응형
'KnockOn Bootcamp' 카테고리의 다른 글
| [2주차 TIL] KnockOn Bootcamp 탐색 알고리즘 (0) | 2025.04.15 |
|---|---|
| [2주차 TIL] KnockOn Bootcamp 정렬 알고리즘 (0) | 2025.04.15 |
| [1주차 TIL] KnockOn Bootcamp 스택&큐 (0) | 2025.04.08 |
| [1주차 TIL] KnockOn Bootcamp 연결 리스트 (0) | 2025.04.07 |
| [1주차 TIL] KnockOn Bootcamp 헤더파일 (0) | 2025.04.06 |
Comments
